Question 1
Which of the following chart symbols represents a preferred channel to port in an IALA B buoyage system?
Your Answer:
Question Not Answered
Correct Answer:

Question 2
Red lateral marks are numbered with even numbers. True or False?
Your Answer:
True
Question 3
Study the following image, it correctly identifies the direction of buoyage when using the IALA Buoyage System A. True or False?
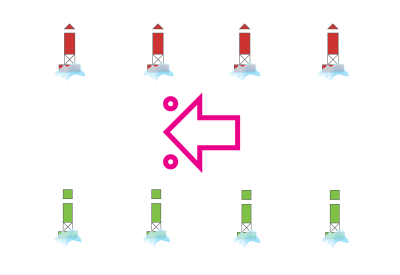
Your Answer:
False
Question 4
Which IALA buoyage system will you be using when entering a harbour in Japan?

Your Answer:
IALA Buoyage System B
Question 5
Study the following image, it correctly identifies the direction of buoyage when using the IALA Buoyage System B. True or False?
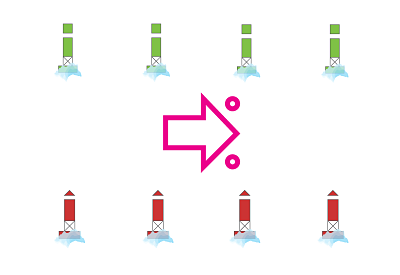
Your Answer:
True
Question 6
The following image correctly shows a channel in IALA Buoyage System B. True or False?

Your Answer:
False
Question 7
An isolated danger buoy has which of the following top mark characteristics?
Your Answer:

Question 8
Which buoys characteristics differ between the 2 IALA buoyage systems?
Your Answer:
Lateral
Question 9
Which cardinal mark has the following colour characteristics?

Your Answer:
North
Question 10
A Safe Water Marker has which of the following top mark characteristics?
Your Answer:

Correct Answer:
